この記事では、Excelでソルバーを使用して、ガウス関数の近似曲線の引き方について、書きたいと思います。
ソルバーの実行(近似曲線を引く)までに、いくつか準備が必要な為、その辺りは過去記事を参考にして頂ければと思います。
この記事では、ソルバーの実行例として、ガウス関数、2つのガウス関数が重なったグラフで近似曲線を求めてみます。
では、どうぞ。
(Excel2016で動作確認しています)
ガウス関数での実行例
ご存知の方も多いと思いますが、ガウス関数は以下の数式で表される正規分布でよく出てくる関数です。
パラメータの μとσからピークの中心と幅が決まります。

ガウス関数の説明はこれぐらいにして、ソルバーの話に入ります。
元データと近似曲線のパラメータを用意する
近似曲性を引きたい元データとそのグラフ、そして、近似曲線のパラメータを用意します。

ここでは、ガウス関数のピークの高さのパラメータとしてaを用意しています。
(元データ-近似曲線)の2乗和を求める
C列に近似曲線のパラメータをガウス関数の式に代入して値を計算します。
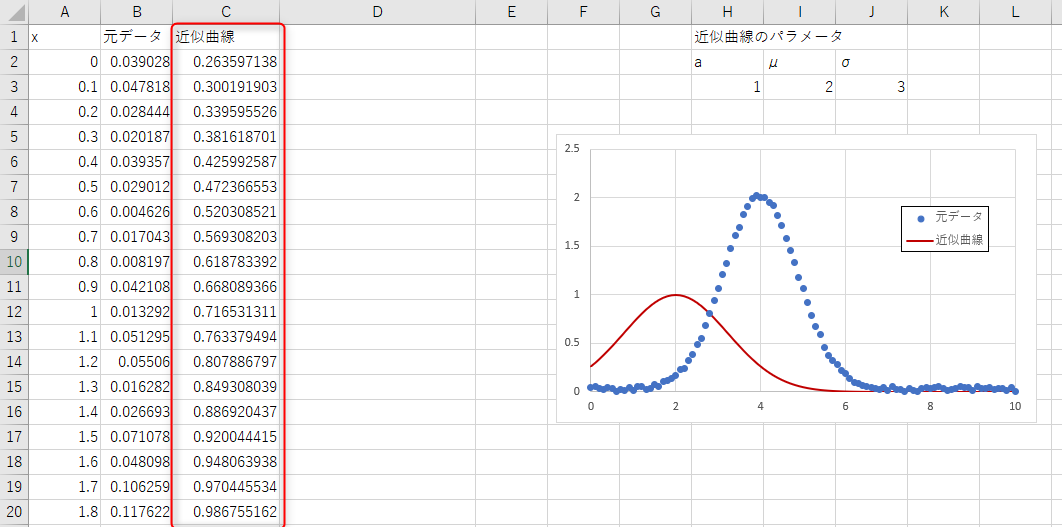
この例ではC2に「=$H$3*EXP(-((A2-$I$3)^2)/$J$3)」と入力しています。
C3以降はコピー。
次にD列に(元データ-近似曲線)の2乗を計算します。
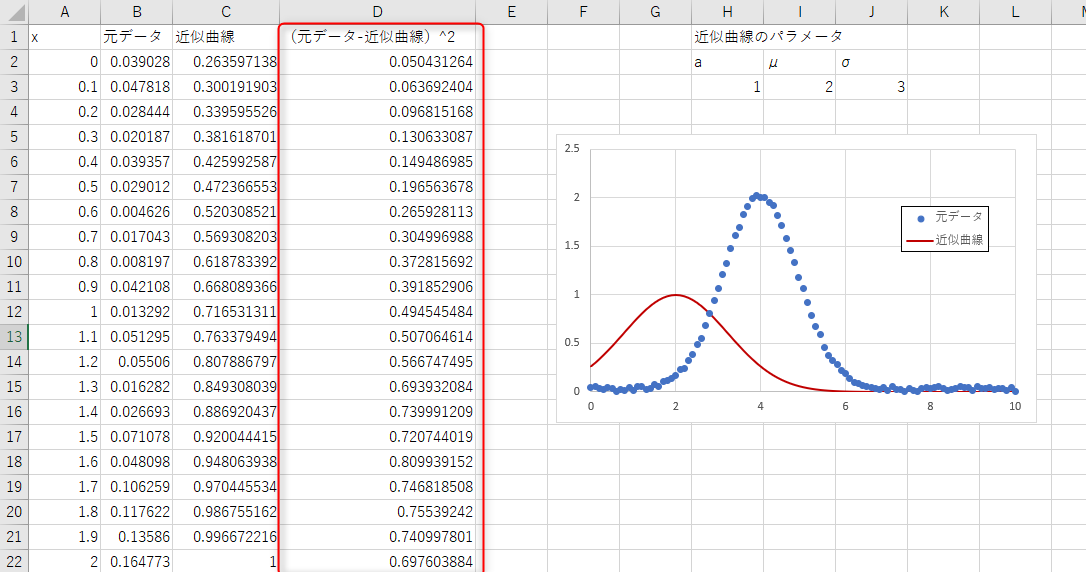
この例ではD2に「=(B2-C2)^2」と入力しています。
D列の合計を計算します。
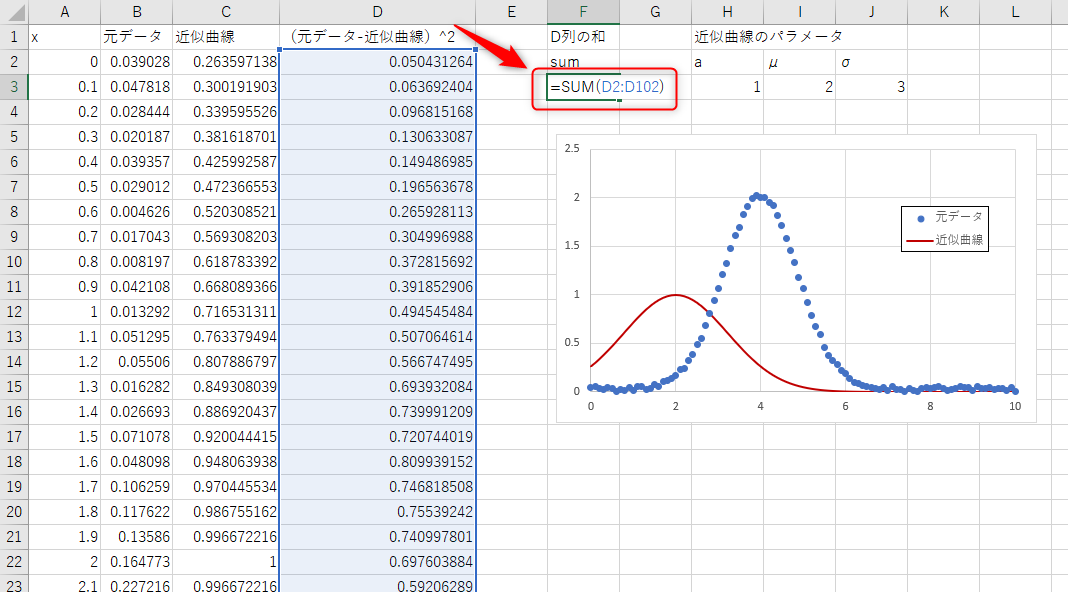
この例ではF3に「=SUM(D2:D102)」と入力しています。
これで(元データ-近似曲線)の2乗和が求まりました。
ソルバーを実行する
いよいよソルバーを実行します。
パラメータを最適化して近似曲線を引きます。
データのタブの左端にあるソルバーを選択します。

ウィンドウが開くので、パラメーターを設定します。
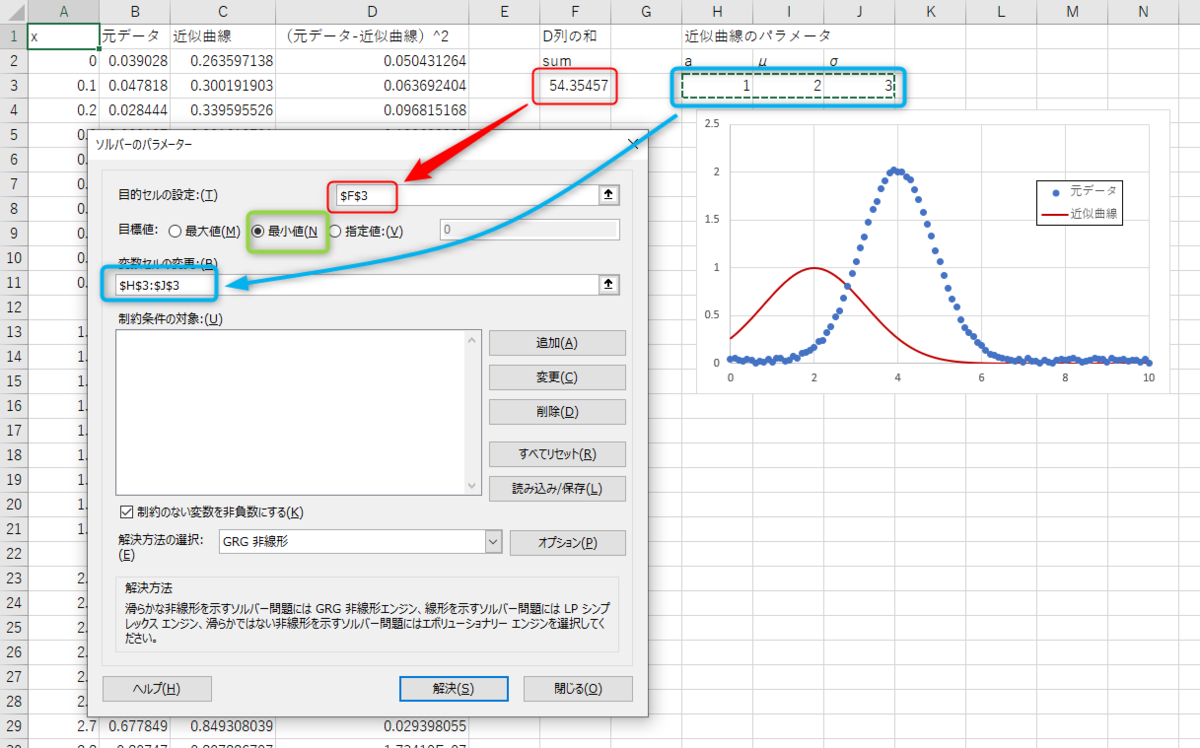
最後に解決を押せば、二乗和が最小になるようにパラメータが最適化されます。
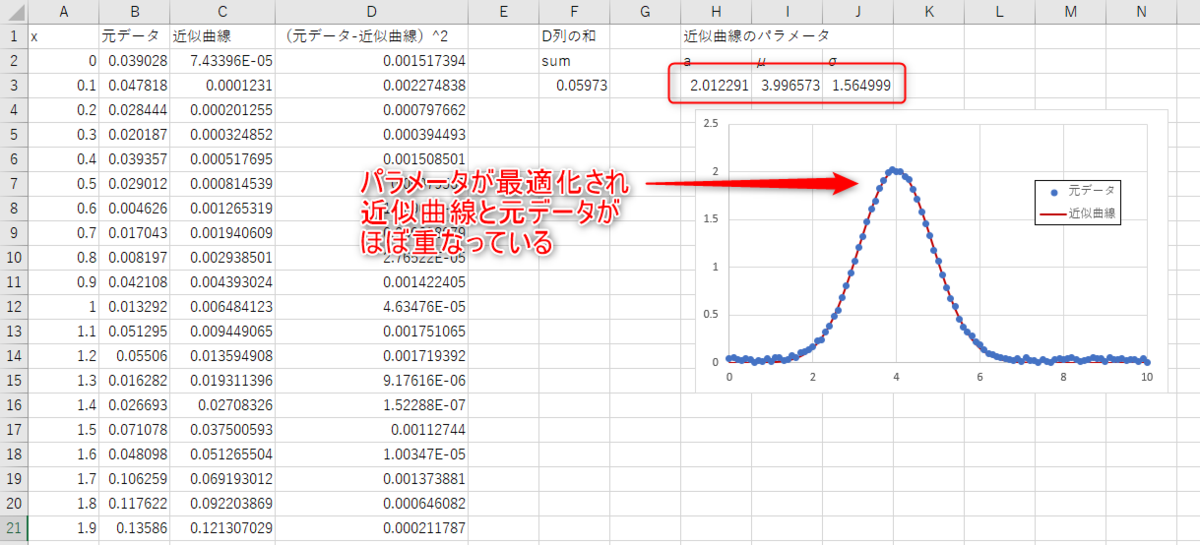
2つのガウス関数が重なったものでの実行例
次はXRDとかでよく見る、2つのピークが重なった場合について考えてみます。
元データは下のグラフ。
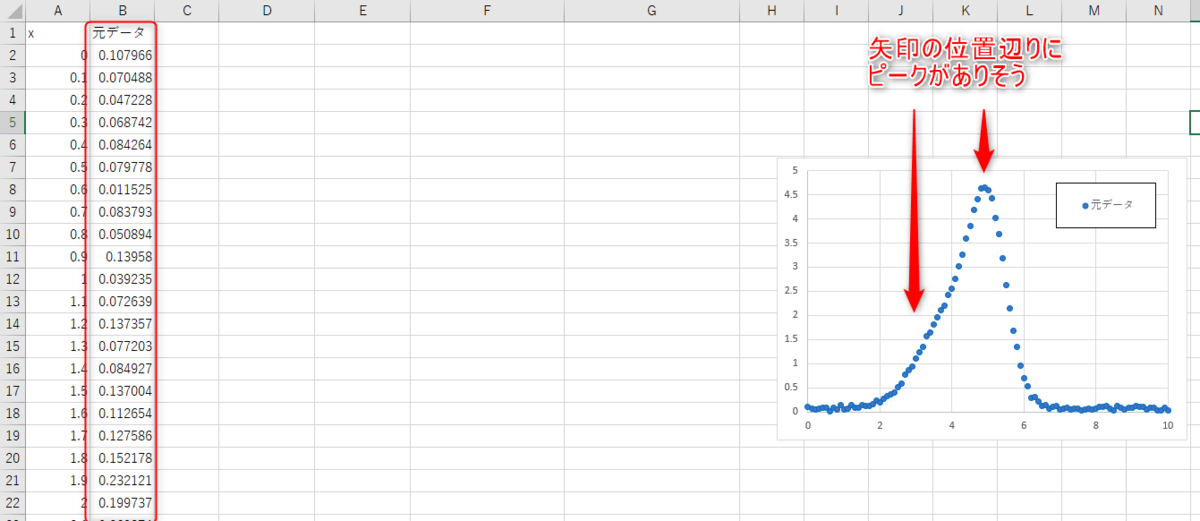
矢印付近に2つのピークがありそうです。
以下の手順は、2つのガウス関数が存在している前提で進めます。
2セット分のパラーメタを用意する
1つ前のガウス関数の例でやった、a、μ、σのパラメータを2セット用意します。
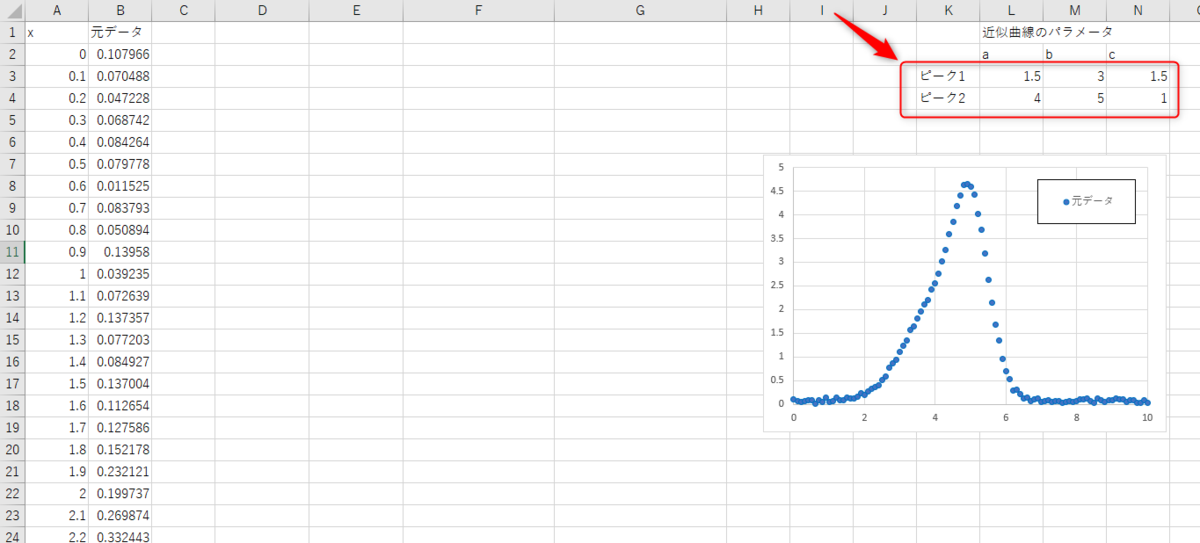
初期値としてなんとなくの値を入れています。
初期値によってソルバーの計算がうまくいかない場合があるので、近い値がわかるならそれを入れるのがいいと思います。
2つの関数の値を計算し、近似曲線の値を用意する
続いて2セット分のピークの関数の値を計算します。
下の例ではD列にピーク1、F列にピーク2の値を計算しています。
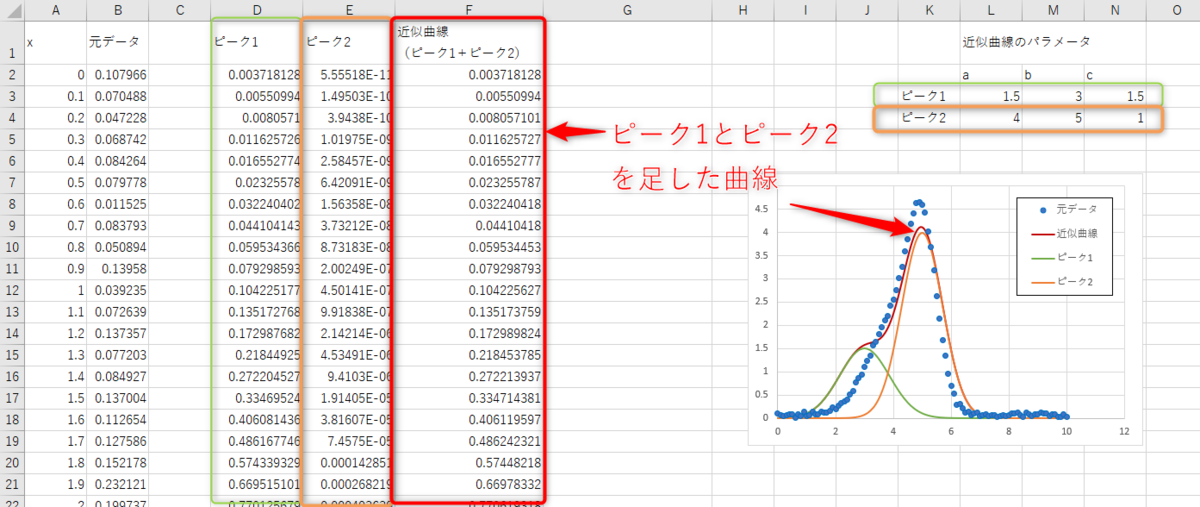
用意したそれぞれのパラメータを使用して計算しており、D2に「=$L$3*EXP(-((A2-$M$3)^2)/$N$3)」と入力しています。
同様にE2には「=$L$4*EXP(-((A2-$M$4)^2)/$N$4)」と入力しています。
F列にはピーク1とピーク2の関数を足しており、この関数が近似曲線になります。
ちょっとそれっぽくなってきました。
(元データ-近似曲線)の2乗和を求める
近似曲線が用意できたので、続いて(元データ-近似曲線)の2乗和を求めます。
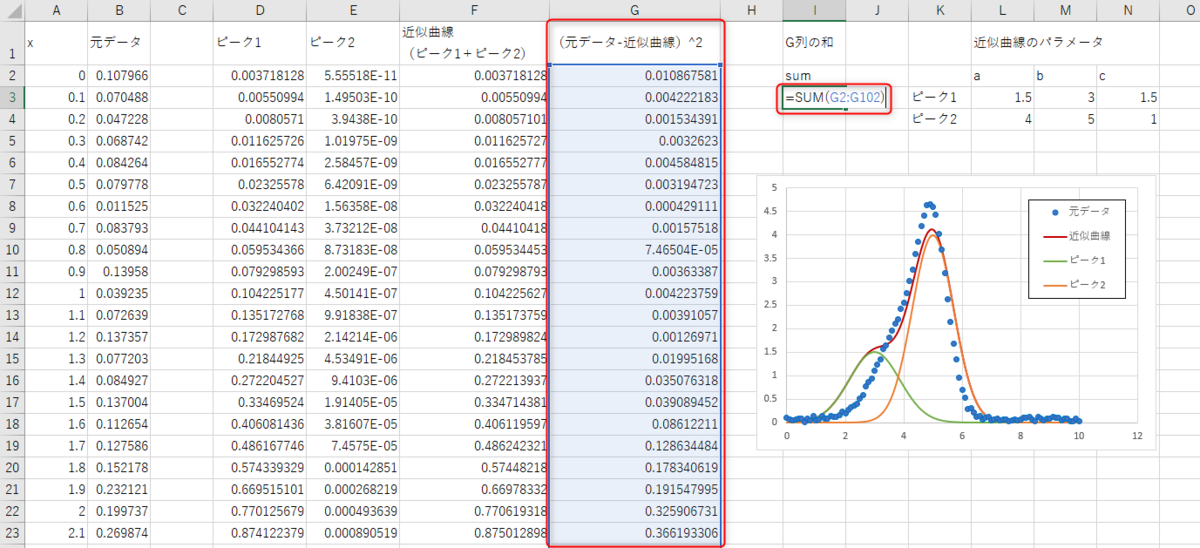
G列に(元データ-近似曲線)の2乗を求めます。
G2には「=(B2-F2)^2」と入力。
I3にG列の和「=SUM(G2:G102)」を計算しています。
ソルバーを実行する
用意ができたので、ソルバーを実行します。
今回はパラメータが2セット分(合計6つ)あるので、それらを変更セルとして設定します(下図の青色四角)。
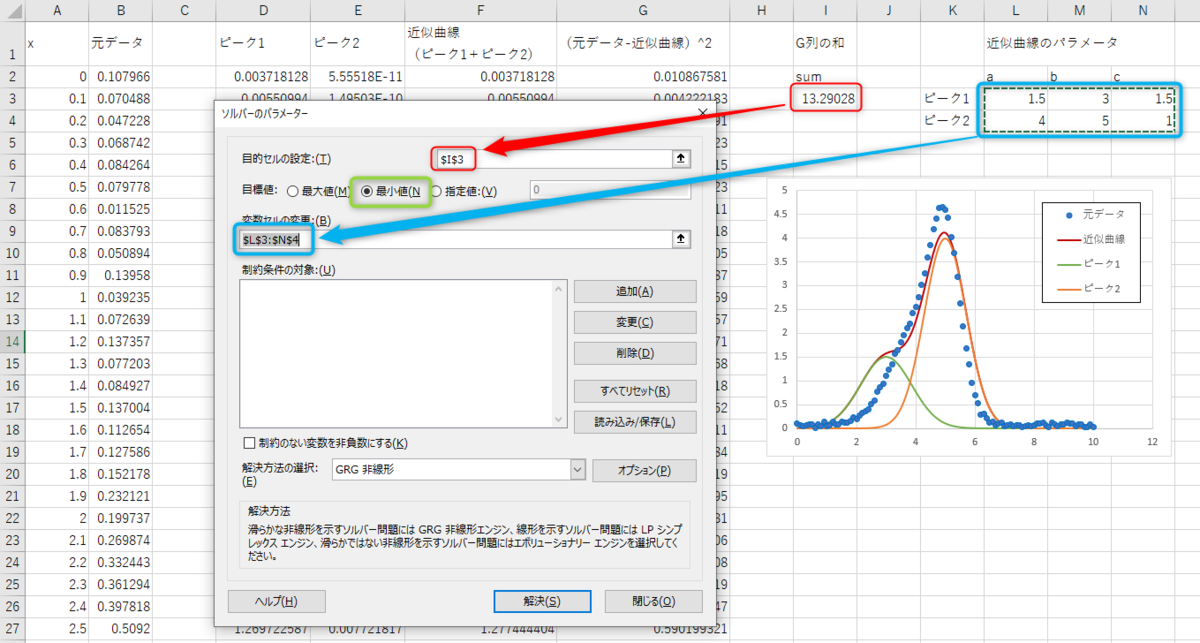
解決を押すと、ソルバーが実行され変数の最適化がされます。
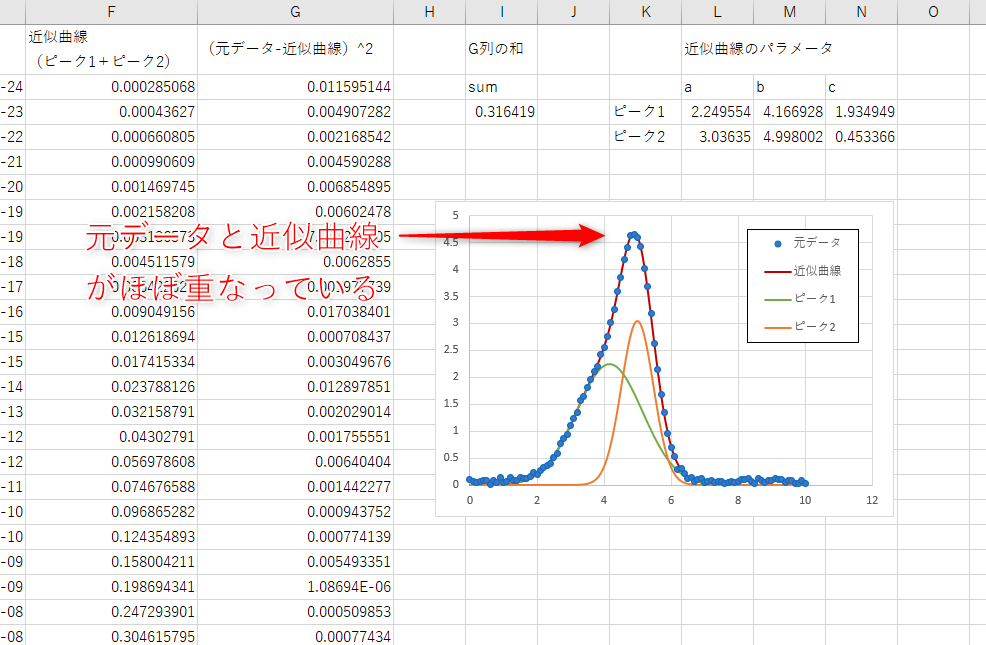
結果が下図。ピーク1とピーク2のパラメータが最適化され、元データと近似曲線がほぼ重なっているのがわかります。すごいぞソルバー!
終わりに
この記事ではソルバー使用例としてガウス関数の例を紹介しましたが、いかがだったでしょうか。
2つのピークが重なった例はあっさり成功して自分でも驚きました。
実際の測定データでうまくいくか分かりませんが、モデルや初期値をうまく設定すればできる可能性があるので、挑戦してみて下さい。
ピークを分解できるとそれぞれのピークが位置がわかるのでありがたいですね。
この記事が誰かのお役に立てたのであれば幸いです。